
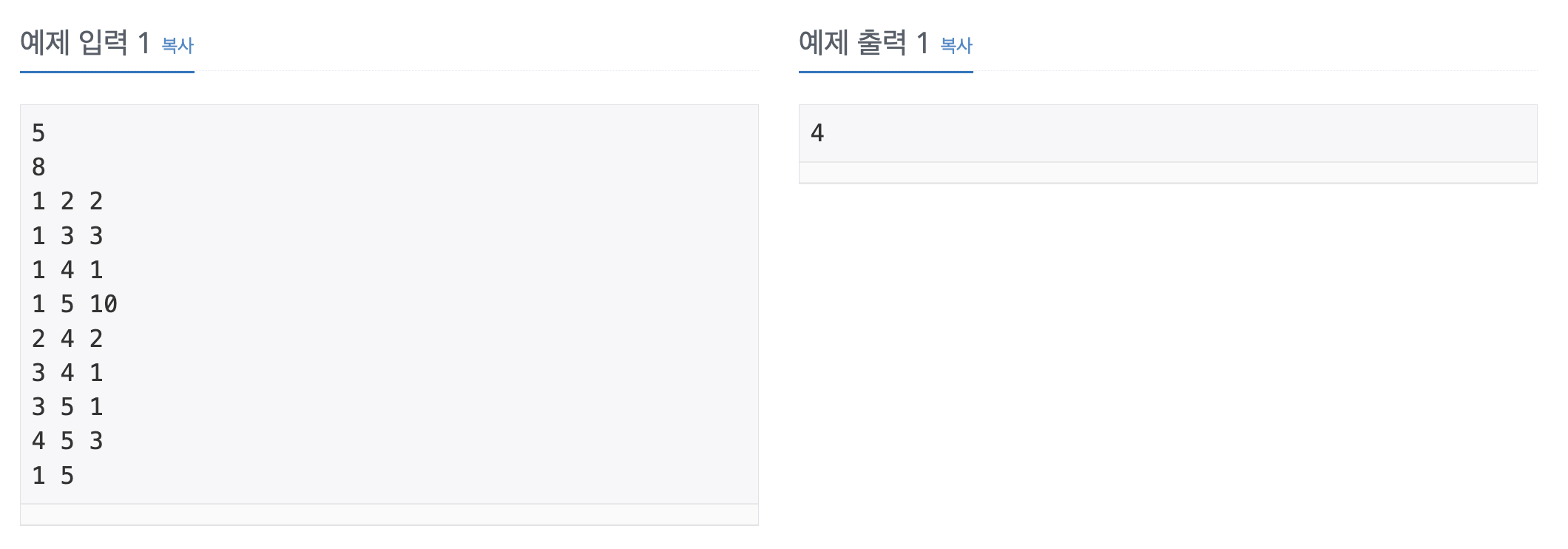
위의 문제는 최소 비용을 구하는 문제로 다익스트라 알고리즘을 활용해서 푸는 대표적인 문제입니다.
먼저 다익스트라 알고리즘의 동작 과정을 간단하게 소개하면 다음과 같습니다.
- 출발 노드와, 도착 노드를 설정
- 알고 있는 모든 거리 값을 부여 (모를 경우 무한(아주 큰 값)으로 설정)
- 출발 노드부터 시작하여, 방문하지 않은 인접 노드를 방문, 거리르 계산한 다음, 현재 알고있는 거리보다 짧으면 해당 값으로 갱신한다.
- 현재 노드에 인접한 모든 미방문 노드까지의 거리를 계산했다면, 현재 노드는 방문한 것이므로, 미방문 집합에서 제거한다.
- 도착 노드가 미방문 노드 집합에서 벗어나면, 알고리즘을 종료한다.
- 우선 순위 큐를 사용하여 지금까지 발견된 가장 짧은 거리의 노드에 대해서 먼저 계산할 수 있으며, 더 긴 거리고 계산 되었을 시 스킵 또한 가능합니다.
N = int(s.readline())
M = int(s.readline())
graph = [[]for _ in range(N+1)]
#graph[A]에 도착도시, 버스비용 저장
for i in range(M):
A,B,C = map(int,s.readline().split())
graph[A].append((B,C))
#출발, 도착지점 입력
start, end = map(int,s.readline().split())
# INF(무한)의 값을 임의로 큰값을 넣어둠
INF = int(1e9)
위의 코드는 입력값 N,M을 받고 graph에 도착 도시와 버스의 비용을 저장합니다. 그리고 다익스트라 알고리즘의 특성처럼 도시까지의 거리를 모르는 값을 INF로 설정해둡니다.
def dijkstra(graph,start):
# 우선순위 큐 생성
heap = []
# 출발점에서 부터 노드까지의 비용을 저장할 배열
distances = [INF] * (N+1)
#1에서 1까지의 거리는 0이므로 0저장
distances[start]=0
#우선순위 큐에 현재 start에 해당하는 dist와 노드 저장
heapq.heappush(heap,[distances[start],start])
while heap:
#heap 에 들어있는 값을 빼서 node,dist라 지정
dist,node =heapq.heappop(heap)
#distances에 INF가 들어있기때문에 dist가 더크면 생략
if distances[node] < dist:
continue
#graph배열에 인접한 노드와 비용을 가져온다
for next_node,next_dist in graph[node]:
#dist + next_dist를 distance에 저장
distance = dist + next_dist
#distance가 distances[next_node]보다 작으면
#distance로 교체하고 heap에 push해준다.
if distance<distances[next_node]:
distances[next_node]=distance
heapq.heappush(heap,[distance,next_node])
#결과값을 distances를 넘겨줌
return distances다익스트라 알고리즘 구현부분입니다.
우선 graph와 start를 파라메터값으로 받아와서 시작점부터 노드를 방문하기 시작합니다.
distances라는 거리를 저장해두는 배열에 최소 비용을 저장해 나가면서 출발점에서 도착점까지의 최소 비용을 구해서 return 해줍니다.
💡전체코드
from sys import stdin as s
import heapq
s = open('input.txt','rt')
def dijkstra(graph,start):
# 우선순위 큐 생성
heap = []
# 출발점에서 부터 노드까지의 비용을 저장할 배열
distances = [INF] * (N+1)
#1에서 1까지의 거리는 0이므로 0저장
distances[start]=0
#우선순위 큐에 현재 start에 해당하는 dist와 노드 저장
heapq.heappush(heap,[distances[start],start])
while heap:
#heap 에 들어있는 값을 빼서 node,dist라 지정
dist,node =heapq.heappop(heap)
#distances에 INF가 들어있기때문에 dist가 더크면 생략
if distances[node] < dist:
continue
#graph배열에 인접한 노드와 비용을 가져온다
for next_node,next_dist in graph[node]:
#dist + next_dist를 distance에 저장
distance = dist + next_dist
#distance가 distances[next_node]보다 작으면
#distance로 교체하고 heap에 push해준다.
if distance<distances[next_node]:
distances[next_node]=distance
heapq.heappush(heap,[distance,next_node])
#결과값을 distances를 넘겨줌
return distances
if __name__=='__main__':
N = int(s.readline())
M = int(s.readline())
graph = [[]for _ in range(N+1)]
#graph[A]에 도착도시, 버스비용 저장
for i in range(M):
A,B,C = map(int,s.readline().split())
graph[A].append((B,C))
#출발, 도착지점 입력
start, end = map(int,s.readline().split())
# INF(무한)의 값을 임의로 큰값을 넣어둠
INF = int(1e9)
#다익스르타 함수 호출 후 결과받아옴
ans=dijkstra(graph,start)
#출발지에서 도착지까지의 최소비용
print(ans[end])'알고리즘 > 백준' 카테고리의 다른 글
| [백준] 18405 경쟁적 전염[Python] (0) | 2023.04.27 |
|---|---|
| [백준] 3055 탈출 [Python] (1) | 2023.04.26 |
| [백준] 2573 빙산 [Python] (0) | 2023.04.25 |
| [백준] 16120 PPAP [Python] (0) | 2023.04.21 |
| [백준] 3190 뱀 [Python] (0) | 2023.04.18 |
