💡다이나믹 프로그래밍(DP)란?
- 다이나믹 프로그래밍은 메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상하는 방법입니다.
- 이미 계산된 결과는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 합니다.
- 다이나믹 프로그맹의 구현은 일반적으로 두 가지 방식(Top Down, Bottom Up)으로 구성됩니다.
다이나믹 프로그래밍의 조건
1. 최적 부분 구조 (Optimal Substructure)
- 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있습니다.
2. 중복되는 부분 문제 (Overlapping Subproblem)
- 동일한 작은 문제를 반복적으로 해결해야 합니다.
다이나믹 프로그래밍 예시
- 피보나치 수열
- n번째 피보나치 수를 f(n)라고 할 때 6번째 피보나치 수 f(6)를 구하는 과정은 다음과 같습니다.
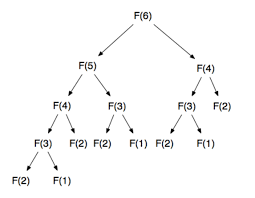
예제 코드
def fibo(x):
if x==1 or x==2:
return 1
else:
return fibo(x-1)+fibo(x-2)
print(fibo(6))
실행결과
8
- 단순 재귀 함수로 피보나치수열을 해결하면 지수 시간 복잡도를 가지게 됩니다.
- 피보나치의 수열의 시간 복잡도는 O(2ᴺ)을 갖게 돼서 많은 연산을 필요로 하는 작업에는 비효율적이라고 볼 수 있습니다.
위의 피보나치 수열을 다이나믹 프로그래밍으로 구현하면 시간복잡도면에서 효율적으로 작동할 수 있습니다.
다이나믹 프로그래밍 방법
1) 메모이제이션(Memoization)
- 한 번 계산한 결과를 메모리 공간에 메모하는 기법입니다.
- 같은 문제를 다시 호출하면 메모했던 결과를 그대로 가져옵니다.
- 값을 기록해 놓는다는 점에서 캐싱이라고도 합니다.
- 시간복잡도는 O(N)입니다.
2) 탑다운(Top Down), 보텀업 (Bottom UP)
- 탑다운(메모이제이션) 방식은 하향식이라고도 하며 보텀업 방식은 상향식이라고 합니다.
- 다이나믹 프로그래밍의 전형적인 형태는 반복문을 사용하는 보텀업 방식입니다.
메모이제이션 - 예제 코드
#한 번 계산된 결과를 메모이제이션하기 위한 리스트 초기화
dp=[0]*100
#피보나치 함수를 재귀함수로 구현(탑다운 다이나믹 프로그래밍)
def fibo(x):
#종료조건(1혹은 2일 때 1을 반환)
if x==1 or x==2:
return 1
#이미 계산한 적 있는 문제라면 그대로 반환
if dp[x]!=0:
return dp[x]
#아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
dp[x]= fibo(x-1)+fibo(x-2)
return dp[x]
print(fibo(99))
실행 결과
218922995834555169026
보텀업 - 예제 코드
#앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
dp =[0] * 100
#첫 번째 피보나치 수와 두 번째 피보나치 수는 1
dp[1]=1
dp[2]=1
n=99
#피보나치 함수 반복문으로 구현(보텀업 다이나믹 프로그래밍)
for i in range(3, n+1):
dp[i] =dp[i-1] + dp[i-2]
print(dp[n])
실행 결과
218922995834555169026
📚다이나믹 프로그래밍 VS 분할 정복
1) 다이나믹 프로그래밍과 분할 정복은 모두 최적 부분 구조를 가질 때 사용할 수 있습니다.
- 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있는 상황
2) 다이나믹 프로그래밍과 분할 정복의 차이점은 부분 문제의 중복입니다.
- 다이나믹 프로그래밍 문제에서는 각 부분 문제들이 서로 영향을 미치며 부분 문제가 중복됩니다.
- 분할 정복 문제에서는 동일한 부분 문제가 반복적으로 계산되지 않습니다.
Reference
- 동빈나 다이나믹 프로그래밍 강의 : https://www.youtube.com/watch?v=5Lu34WIx2Us
https://www.youtube.com/watch?v=5Lu34WIx2Us
'알고리즘 > 개념' 카테고리의 다른 글
| [알고리즘] 그리디 알고리즘 (0) | 2023.04.28 |
|---|---|
| [알고리즘] 위상 정렬 (0) | 2023.04.26 |
| [알고리즘] Union - Find 알고리즘 (0) | 2023.04.21 |
| [알고리즘] 최소 신장 트리(MST) : 프림 알고리즘 (0) | 2023.04.21 |
| [알고리즘] 최소 신장 트리(MST) : 크루스칼 알고리즘 (0) | 2023.04.21 |
