[자료구조] 레드블랙트리(Red-Black tree)

RB-TREE

 

1️⃣  레드 블랙 트리(RB Tree)

- 레드 블랙 트리는 이진 탐색 트리(BST)의 한 종류로 스스로 균형을 잡는 트리입니다.

- BST의 단점을 개선하고 모든 노드의 색깔은 Red or Black 입니다.

- 시간복잡도는 O(logN)입니다.

 

 

 

2️⃣  레드 블랙 트리의 다섯가지 속성

1) 모든 노드는 Red or Black이다.

2) 루트 노드는 Black이다.

3) 모든 리프 노드(NIL)들은 Black이다.

4) Red 노드의 자식은 Black이다. -> Red가 연속적으로 존재할 수 없다.

5) 모든 리프 노드에서 Black Depth는 같다. (자기 자신은 카운트에서 제외)

 

💡NIL 노드란?

- 존재하지 않음을 의미하는 노드로 자녀가 없을 때 자녀를 nil 노드로 표기한다.

- 값이 있는 노드와 동등하게 취급하고 RB 트리에서 leaf 노드는 NIL 노드를 의미한다.

 

 

3️⃣  RB 트리 삽입 단계

1. 삽입 전 RB 트리 속성을 만족한 상태여야 한다.
2. 삽입 방식은 일반적인 BST와 동일하다.
3. 삽입 후 RB 트리 위반 여부를 확인한다.
4. RB 트리 속성을 위반했다면 재조정한다.
5. RB 트리 속성을 다시 만족한다.

 

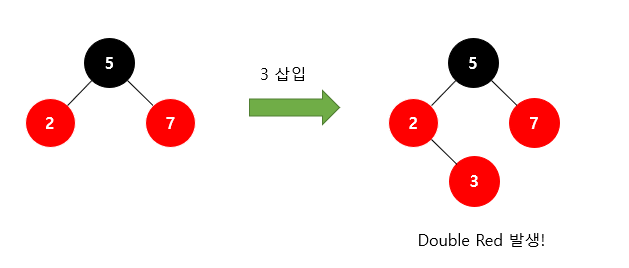
레드-블랙 트리에 새로운 노드를 삽입할 때 새로운 노드는 항상 빨간색으로 삽입한다.

이렇게 되면 4번 조건이 위배되는 상황이 발생한다. 즉, 빨간색 노드가 연속으로 2번 나타날 수 있다(Double Red)

 

레드 블랙 트리는 이러한 Double Red 문제를 해결하기 위해 2가지 전략을 사용한다.

 

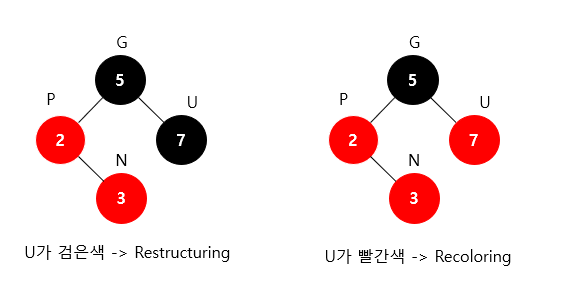
조상 노드를 G, 부모 노드를 P, 삼촌 노드를 U, 새로 삽입 할 노드를 N이라고 하자.

 

Double Red가 발생했을 때

• 삼촌 노드가 검은색이라면 -> Restructuring을 수행하면 된다.
• 삼촌 노드가 빨간색이라면 -> Recoloring을 수행하면 된다.

 

Restructuring과정

• 새로운 노드(N), 부모 노드(P), 조상 노드(G)를 오름차순으로 정렬한다.
• 셋 중 중간값을 부모로 만들고 나머지 둘을 자식으로 만든다.
• 새로 부모가 된 노드를 검은색으로 만들고 나머지 자식들을 빨간색으로 만든다. 
  
  

Recoloring과정

• 새로운 노드(N)의 부모(P)와 삼촌(U)를 검은색으로 바꾸고 조상(G)을 빨간색으로 바꾼다.
• 조상(G)이 루트 노드라면 검은색으로 바꾼다.
• 조상(G)을 빨간색으로 바꿨을 때 또다시 Double Red가 발생한다면 또다시 Restructuring 혹은 Recoloring을 진행해서 Double Red 문제가 발생하지 않을 때까지 반복한다.

 

4️⃣  RB 트리 삭제 단계

1. 삭제 전 RB 트리 속성을 만족한 상태여야한다.
2. 삭제 방식은 일반적인 BST와 동일하다.
3. 삭제 후 RB 트리 속성 위반 여부를 확인한다.
4. RB 트리 속성을 위반했다면 재조정한다.
5. RB 트리 속성을 다시 만족한다.

💡 RB트리에서 노드를 삭제할 때 어떤 색이 삭제되는지가 속성 위반 여부를 확인할 때 매우 중요하다.

 

 

삭제 과정

• 삭제하려는 노드의 자녀가 없거나 하나라면 삭제되는 색은 삭제되는 노드의 색입니다.
• 삭제하려는 노드의 자녀가 둘이라면 삭제되는 색은 삭제되는 노드의  *successor의 색입니다.
• *successor란 해당 노드의 오른쪽 자녀의 값들 중 가장 작은 값을 의미한다.

 

---

• 삭제되는 색이 Red 라면 문제 없다.
• 삭제되는 색이 Black일 때 삭제되는 색이 있던 위치를 대체한 노드에 extra black을 부여합니다.
• 대체한 노드가 Red-and-Black이 됐다면 Black으로 바꿔주면 끝.
• 대체한 노드가 doubly black이 됐다면 case 1,2,3,4중에 하나로 해결